文章目录
- 主成分分析(Principal Component Analysis,PCA)是一种常用的无监督学习方法
- 利用正交变换把由
线性相关变量表示的观测数据转换为少数几个由线性无关变量表示的数据,线性无关的变量 称为 主成分 - 主成分的个数
通常小于原始变量的个数,所以PCA属于降维方法 - 主要用于发现数据中的
基本结构,即数据中变量之间的关系,是数据分析的有力工具,也用于其他机器学习方法的前处理 - PCA属于
多元统计分析的经典方法
1. 总体主成分分析
第一轴选取方差最大的轴 y1
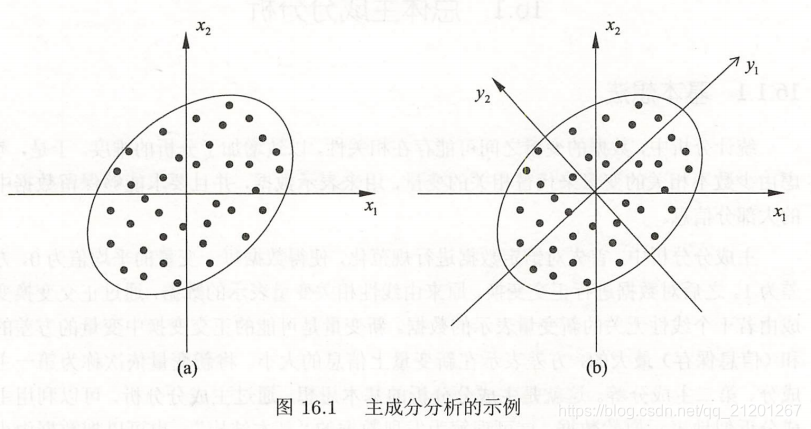
主成分分析 的主要目的是降维,所以一般选择 k( k ≪ m k\ll m k≪m)个主成分(线性无关变量)来代替m个原有变量(线性相关变量),使问题得以简化,并能保留原有变量的大部分信息(原有变量的方差)。
在实际问题中,不同变量可能有不同的量纲,直接求主成分有时会产生不合理的结果。
为了消除这个影响,常常对各个随机变量实施规范化,使其均值为0,方差为1。
主成分分析的结果可以用于其他机器学习方法的输入。
- 将样本点投影到以主成分为坐标轴的空间中,然后应用聚类算法,就可以对样本点进行聚类
定义:
假设 x \pmb x xxx 为 m m m 维随机变量,均值为 μ \mu μ,协方差矩阵为 Σ \Sigma Σ
随机变量 x \pmb x xxx 到 m m m 维随机变量 y \pmb y yyy 的线性变换
y i = α i T x = ∑ k = 1 m α k i x k , i = 1 , 2 , . . . , m y_i = \alpha_i^T \pmb x = \sum\limits_{k=1}^m \alpha_{ki}x_k, \quad i=1,2,...,m yi=αiTxxx=k=1∑mαkixk,i=1,2,...,m
其中 α i T = ( α 1 i , α 2 i , . . . , α m i ) \alpha_i^T = (\alpha_{1i},\alpha_{2i},...,\alpha_{mi}) αiT=(α1i,α2i,...,αmi)
如果该线性变换满足以下条件,称之为总体主成分:
- α i T α i = 1 , i = 1 , 2 , . . . , m \alpha_i^T\alpha_i = 1, i = 1, 2,...,m αiTαi=1,i=1,2,...,m
- c o v ( y i , y j ) = 0 ( i ≠ j ) cov (y_i,y_j) = 0(i \neq j) cov(yi,yj)=0(i=j)
- y 1 y_1 y1 是 x \pmb x xxx 的所有线性变换中
方差最大的, y 2 y_2 y2 是与 y 1 y_1 y1 不相关的 x \pmb x xxx 的所有线性变换中方差最大的,以此类推, y 1 , y 2 , . . . , y m y_1,y_2,...,y_m y1,y2,...,ym 称为第一主成分…第 m m m 主成分
假设 x \pmb x xxx 是 m m m 维随机变量,其协方差矩阵 Σ \Sigma Σ 的特征值分别是 λ 1 ≥ λ 2 ≥ . . . ≥ λ m ≥ 0 \lambda_1 \ge \lambda_2 \ge ... \ge \lambda_m \ge 0 λ1≥λ2≥...≥λm≥0,特征值对应的单位特征向量分别是 α 1 , α 2 , . . . , α m \alpha_1,\alpha_2,...,\alpha_m α1,α2,...,αm,则 x \pmb x xxx 的第 i i i 主成分可写作:
y i = α i T x = ∑ k = 1 m α k i x k , i = 1 , 2 , . . . , m y_i = \alpha_i^T \pmb x = \sum\limits_{k=1}^m \alpha_{ki}x_k, \quad i=1,2,...,m yi=αiTxxx=k=1∑mαkixk,i=1,2,...,m
并且, x \pmb x xxx 的第 i i i 主成分的方差是协方差矩阵 Σ \Sigma Σ 的第 i i i 个特征值,即:
v a r ( y i ) = α i T Σ α i = λ i var (y_i) = \alpha_i^T\Sigma\alpha_i = \lambda_i var(yi)=αiTΣαi=λi
主成分性质:
-
主成分 y \pmb y yyy 的
协方差矩阵是对角矩阵 c o v ( y ) = Λ = d i a g ( λ 1 , λ 2 , . . . , λ m ) cov(\pmb y) = \Lambda = diag(\lambda_1,\lambda_2,...,\lambda_m) cov(yyy)=Λ=diag(λ1,λ2,...,λm) -
主成分 y \pmb y yyy 的
方差之和等于随机变量 x \pmb x xxx 的方差之和
∑ i = 1 m λ i = ∑ i = 1 m σ i i \sum\limits_{i=1}^m \lambda_i = \sum\limits_{i=1}^m \sigma_{ii} i=1∑mλi=i=1∑mσii
其中 σ i i \sigma_{ii} σii 是 x i x_i xi 的方差,即协方差矩阵 Σ \Sigma Σ 的对角线元素 -
主成分 y k y_k yk 与变量 x i x_i xi 的 相关系数 ρ ( y k , x i ) \rho(y_k,x_i) ρ(yk,xi) 称为因子负荷量(factor loading),它表示第 k k k 个主成分 y k y_k yk 与变量 x i x_i xi 的相关关系,即 y k y_k yk 对 x i x_i xi 的
贡献程度
ρ ( y k , x i ) = λ k α i k σ i i , k , i = 1 , 2 , . . . , m \rho(y_k, x_i) = \frac{\sqrt{\lambda_k}\alpha_{ik}}{\sqrt{\sigma_{ii}}},k,i=1,2,...,m ρ(yk,xi)=σii λk αik,k,i=1,2,...,m
2. 样本主成分分析
是基于样本协方差矩阵的主成分分析
给定样本矩阵 X X X

X X X 的样本协方差矩阵
S = [ s i j ] m × n , s i j = 1 n − 1 ∑ k = 1 m ( x i k − x ˉ i ) ( x j k − x ˉ j ) i = 1 , 2 , . . . , m , j = 1 , 2 , . . . , m , 其 中 x ˉ i = 1 n ∑ k = 1 n x i k S = [s_{ij}]_{m \times n}, \quad s_{ij} = \frac{1}{n-1}\sum\limits_{k=1}^m(x_{ik}-\bar x_i)(x_{jk}-\bar x_j)\\ i = 1,2,...,m,\quad j = 1,2,...,m, 其中 \bar x_i = \frac{1}{n}\sum\limits_{k=1}^n x_{ik} S=[sij]m×n,sij=n−11k=1∑m(xik−xˉi)(xjk−xˉj)i=1,2,...,m,j=1,2,...,m,其中xˉi=n1k=1∑nxik
给定样本 X X X,考虑 x \pmb x xxx 到 y \pmb y yyy 的线性变换 y = A T x \pmb y = A^T \pmb x yyy=ATxxx

如果满足以下条件,称之为样本主成分:
- 样本第一主成分 y 1 = α 1 T x y_1 = \alpha_1^T \pmb x y1=α1Txxx 是在 α 1 T α 1 = 1 \alpha_1^T\alpha_1 = 1 α1Tα1=1 条件下,使得 α 1 T x j ( j = 1 , 2 , . . . , n ) \alpha_1^T \pmb x_j (j=1,2,...,n) α1Txxxj(j=1,2,...,n) 的样本方差 α 1 T S α 1 \alpha_1^TS\alpha_1 α1TSα1 最大的 x \pmb x xxx 的线性变换,以此类推。
- 样本第 i i i 主成分 y i = α i T x y_i = \alpha_i^T \pmb x yi=αiTxxx 是在 α i T α i = 1 \alpha_i^T\alpha_i = 1 αiTαi=1 和 α i T x j \alpha_i^T\pmb x_j αiTxxxj 与 α k T x j ( k < i , j = 1 , 2 , . . . , n ) \alpha_k^T \pmb x_j \quad(k < i,j = 1,2,...,n) αkTxxxj(k<i,j=1,2,...,n)的样本协方差 α k T S α i = 0 \alpha_k^TS\alpha_i=0 αkTSαi=0 条件下,使得 α i T x j ( j = 1 , 2 , . . . , n ) \alpha_i^T \pmb x_j (j=1,2,...,n) αiTxxxj(j=1,2,...,n) 的样本方差 α i T S α i \alpha_i^TS\alpha_i αiTSαi 最大的 x \pmb x xxx 的线性变换
3. 主成分分析方法
3.1 相关矩阵的特征值分解算法
- 针对 m × n m \times n m×n 样本矩阵 X X X ,求样本
相关矩阵R = 1 n − 1 X X T R = \frac{1}{n-1}XX^T R=n−11XXT - 再求样本
相关矩阵的 k k k 个特征值和对应单位特征向量,构造正交矩阵
V = ( v 1 , v 2 , . . . , v k ) V = (v_1,v_2,...,v_k) V=(v1,v2,...,vk) - V V V 的每一列对应一个主成分,得到 k × n k \times n k×n 样本
主成分矩阵Y = V T X Y=V^TX Y=VTX
3.2 矩阵奇异值分解算法
- 针对 m × n m \times n m×n 样本矩阵 X X X , X ′ = 1 n − 1 X T X' = \frac{1}{\sqrt{n-1}}X^T X′=n−1 1XT
- 对矩阵 X X X 进行
截断奇异值分解,保留 k k k 个奇异值、奇异向量
得到 X ′ = U S V T X' = USV^T X′=USVT - V V V 的每一列对应一个主成分,得到 k × n k \times n k×n 样本
主成分矩阵Y = V T X Y=V^TX Y=VTX
4. sklearn.decomposition.PCA
sklearn.decomposition.PCA 官网介绍
class sklearn.decomposition.PCA(n_components=None, copy=True,
whiten=False, svd_solver='auto', tol=0.0,
iterated_power='auto', random_state=None)
参数:
n_components:保留主成分个数,没有赋值,特征个数不变
属性:
components_:主成分
explained_variance_:各特征方差
explained_variance_ratio_:各特征方差百分比
singular_values_:主成分的奇异值
n_components_:保留特征个数
方法:

import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
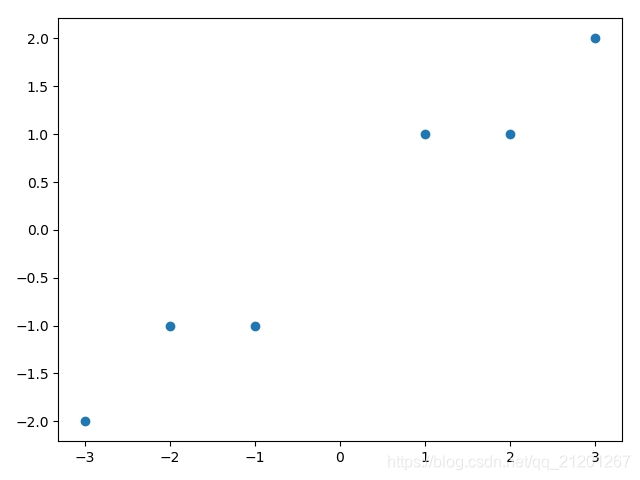
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
plt.scatter(X[:, 0], X[:, 1])
plt.show()
for n in range(1, 3):
print("PCA n_components = {}".format(n))
pca = PCA(n_components=n)
pca.fit(X)
print("特征方差")
print(pca.explained_variance_)
print("特征方差占比")
print(pca.explained_variance_ratio_)
print("主成分奇异值")
print(pca.singular_values_)
print("主成分")
print(pca.components_)
print("主成分个数")
print(pca.n_components_)
PCA n_components = 1
特征方差
[7.93954312]
特征方差占比
[0.99244289]
主成分奇异值
[6.30061232]
主成分
[[-0.83849224 -0.54491354]]
主成分个数
1
PCA n_components = 2
特征方差
[7.93954312 0.06045688]
特征方差占比
[0.99244289 0.00755711]
主成分奇异值
[6.30061232 0.54980396]
主成分
[[-0.83849224 -0.54491354]
[ 0.54491354 -0.83849224]]
主成分个数
2




